Myers差分算法
目录
前言
最近在编写一个小工具,文本对比工具,类似于 git diff 或者下面这些网站
- https://text-compare.com/zh-hans/
- https://www.jq22.com/textDifference
- https://www.diffchecker.com/zh-Hans/
但是 git diff 命令行没有网页看起来方便,而网站的话广告又太多了,所以就打算写一个客户端的小工具软件。
文本比较涉及到的一个著名的算法就是 Myers 算法,由 Eugene W. Myers 在 1986 年发表。本文详细介绍下该算法的原理和实现。
差异
对于两个文本有什么差异之前,我们必须要稍微定义下,什么是二者的差异。
在 Myers 算法中,差异大概可以这么描述:一个文本(序列 A)转换成另一个文本(序列 B)所需要的最少的编辑操作。
算法中对于编辑操作作了限制,允许三种操作:
- 删除,delete,从序列 A 中删除元素
- 插入,insert,向序列 A 中插入新的元素
- 匹配,match,序列 A 和序列 B 当前的元素相同时,无需操作,向前移动,检查下一个元素
算法没有定义替换的概念,替换被视为(删除+插入)。
举个简单的例子,假设序列 A = compliant,序列 B = complaint,从序列 A 转换到序列 B 这个过程,所用的所有操作就是我们所说的“差异”。
转换
A = compliant
B = complaint
在仅允许 delete,insert,match 三个操作的情况下,有多少种转换方式?
第一种
最简单直接的方式就是,对 A 的每一个字符执行 delete 操作,变成空字符串后,在执行 insert 操作,变成 B。
第二种
A 和 B 的前 5 个字符(compl)相等,所以可以对前 5 个字符执行 match 操作。
从第 6 个字符开始不一样了,所以我们可以删除第 6 及其之后的字符,然后再执行 insert 操作,变成 B。
第三种
和第二种类似,前面相同的字符执行 match 操作。
A(6)=i,B(6)=a,所以 A 在第 6 个字符插入 a,此时,A 变成 complaiant。
A(7)=i,B(7)=i,match。
A(8)=a,B(8)=n,执行删除操作,删除 A 的第 8 个字符,此时,A 变成 complaint。
A(9)=t,B(9)=t,match。
第四种
前面相同的字符执行 match 操作。
A(6)=i,B(6)=a,执行删除操作,此时,A 变成 complant。
A(6)=a,B(6)=a,match。
A(7)=空,B(7)=i,执行插入操作,插入字符 i,此时,A 变成 complaint。
A(8)=n,B(8)=n,match。
A(9)=t,B(9)=t,match。
可以看到,不止一种方式可以使用这三个操作,把序列 A 转换成序列 B,每一种的操作方式和步骤不尽相同,所以会存在好的解法和糟糕的解法,我们需要一种度量方式,来衡量执行步骤的好坏。
衡量标准
Myers 算法使用的标准是 最短编辑距离 ,就是使用最少的编辑步骤完成转换,即最少的插入和删除次数。
编辑图
Myers 算法巧妙的将比较序列 A 和序列 B 差异的问题,转换成了序列 A 变成序列 B 的最少需要多少编辑步骤可以完成的问题。
同时,它使用了一个有向无环编辑图来表示序列 A 是如何变成序列 B 的,为了形成编辑图,Myers 沿 x 轴从左到右排列序列 A,然后,沿 y 轴从上到下排列序列 B,并从它们投影出水平和垂直的正交网格。从左上角开始,目标是走到右下角,左上角到右下角的每一次移动都对应于序列 A 上的编辑指令。
移动方向对应的编辑命令如下:
- 水平向右移动表示从序列 A 中删除元素
- 垂直移动表示向序列 A 插入新元素
- 如果序列 A 和序列 B 元素等效,则允许对角线移动。
以图片的形式,展示以下上一节的四个转换方式。
方式一:
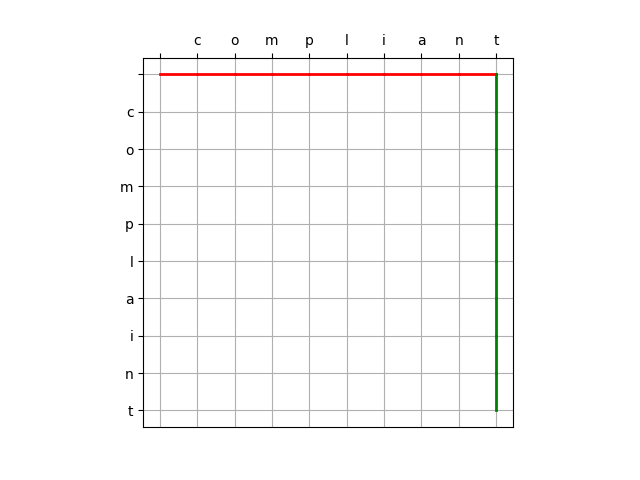
方式二:
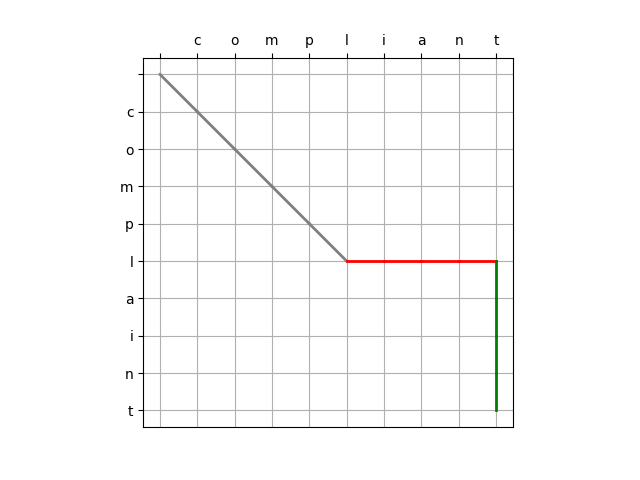
方式三:
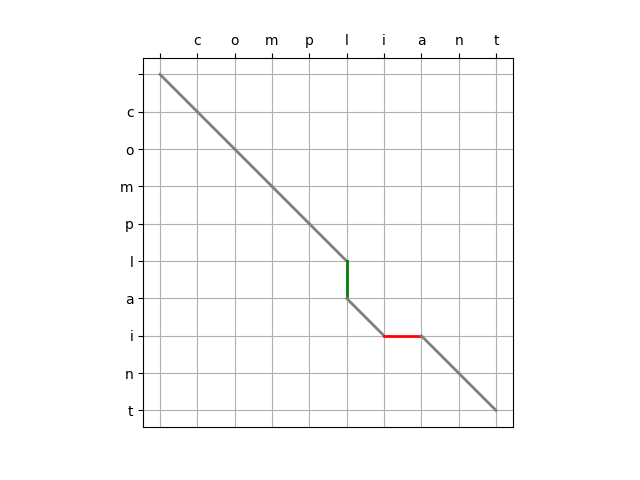
方式四:
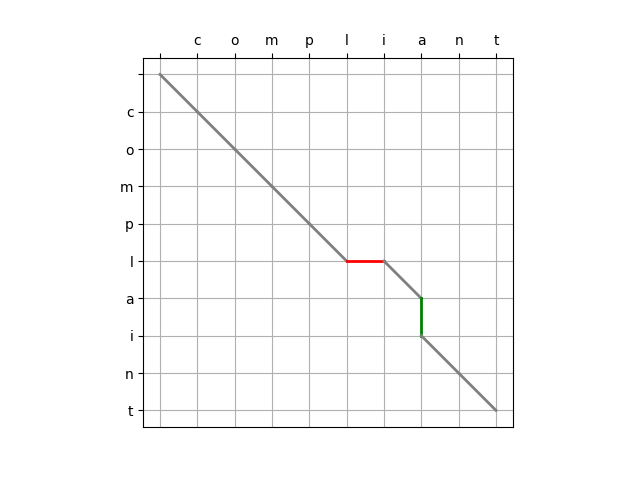
参考
- http://www.xmailserver.org/diff2.pdf
- https://www.nathaniel.ai/myers-diff/
- https://cloud.tencent.com/developer/article/2367282